python入門: 14. 2変数関数と曲面
行列を画像として表示する
巨大な行列は, 個々の成分を数値で表すのではなく, 点の色や明るさとして表すことで, 画像として表すことができる。何のことかわからない, という人も大丈夫。以下, やってみよう。pythonシェルで以下を打っていこう:
import numpy as np import matplotlib.pyplot as plt A=np.reshape(np.arange(0,10000),(100,100)) plt.imshow(A) plt.show()
すると, なんか虹っぽい絵が出ただろう:
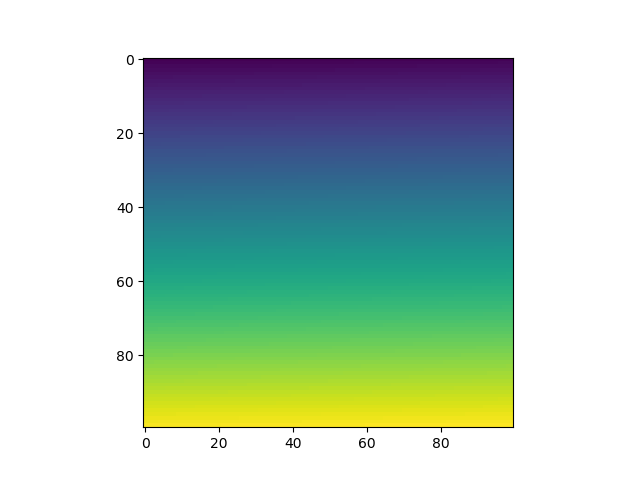
何をやったか説明しよう。
a=np.reshape(np.arange(0,10000),(100,100))
は, 前節で似たようなことをやったのを覚えているだろうか? np.arange(0,10000)は, 0から9999までの整数値を並べた「np.ndarrayクラスのインスタンス」である。それをnp.reshape()という関数に入れている。この関数は, 行列(np.ndarray)の数値はそのままで形(行数と列数の組み合わせというか配分)を変える関数である。ここでは, (100, 100)と指定しており, つまり100行100列の行列にしてくれ, という意味である。実際, 以下を打ってみよう:
A.shape
と打ってみると, それが確認できるだろう。
plt.imshow()というのは, 行列(np.ndarrayクラスのインスタンス)を画像として描画する関数。plt.show()はそれをディスプレイに表示する関数である(前回も使った!)。値が小さいところを青く, zが大きいところを赤く着色されている。この行列は上の方が値が小さく, 下に行くほど値が大きくなるので, 同色が概ね水平に重なるような絵になっている。
では, 以下を試してみよう:
plt.imshow(A.T) plt.show()
色の層がこんどは縦になった:
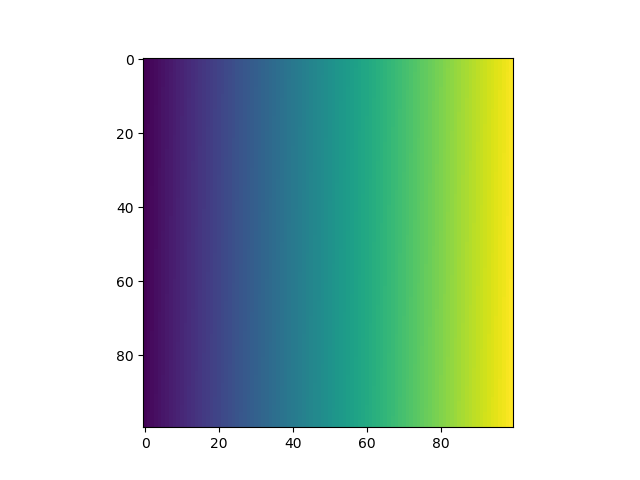
なぜだろう? ヒント: .Tというのは「転置」を意味する。
では, 以下をやってみよう:
A=np.arange(0,100) B=np.tensordot(A, A, 0) plt.imshow(B) plt.show()
さきほどとちょっと変わった。ポイントは, B=np.tensordot(A, A, 0)である。詳しいことは省くが, これはベクトルAとAの転置の積である(列ベクトルと行ベクトルの積)。その結果であるBを見てみよう:
B
i行j列の成分は, i*jに等しくなっている。これが「ベクトルAとAの転置の積」ということから納得できるだろうか? (行列をちゃんと勉強していればわかるはず!!)
2変数関数のグラフ(曲面)を描く
では, 以下をやってみよう:
x, y=np.meshgrid(np.arange(-2, 2, 0.04), np.arange(2, -2, -0.04)) x y
このxは, 左から右に-2から2(の手前)まで徐々に値が大きくなる行列で, yは, 下から上に-2から2(の手前)まで徐々に値が大きくなる行列である。それぞれを表示して確認してみよう。ここではちょっと新しいワザを使って, 2つの図を並べて表示してみる:
plt.subplot(121) plt.imshow(x) plt.subplot(122) plt.imshow(y) plt.show()
さて, このxとyを使って, 2変数関数z=f(x, y)の「グラフ」, つまり「曲面」が描ける! 以下を打ってみよう:
z=x**2+y**2 plt.imshow(z) plt.show()
これは, zが小さいところを青く, zが大きいところを赤く着色して関数z(x, y)を表したものである。これを投稿線でも表してみよう:
plt.contour(x, y, z) plt.show()
これは地形図のようなものである。
ここで見たのは「回転放物面」という曲面である。実際, この曲面の, y=0での切断面を見てみよう。y=0となるのは, zの第0要素がちょうど50番目あたりの行であり, それは
z[50, :]
で取り出すことができる(添字部分に:を置くと, 該当する成分すべて, という意味になる)。プロットしてみよう:
plt.plot(x[50,:], z[50, :]) plt.show()
きれいな放物線が描けるだろう!!
では, 以下はどうだろう?
z=np.exp(-(x**2+y**2)) plt.subplot(121) plt.imshow(z) plt.subplot(122) plt.contour(x, y, z) plt.show()
これはガウス関数の2次元版である。回転放物面と大差ないように思うかも知れないが, 切断面を見てみよう:
plt.plot(x[50,:], z[50, :]) plt.show()
このような釣鐘型が回転してできたような山型の曲面である。
レポート課題14-1: 以下の各曲面を描け。例: z=x*yの曲面は, plt.imshow(x*y); plt.show()とすればよい。
z=x*y z=x**2-y**2 z=(sin x)*(sin y) z=(sin 2x)*(sin 3y) z=(sin 10x)*(sin 10y)/(xy)
Keyword(s):
References:[python入門]