開水路の水面形

問題設定

　以下の図のように、水路を水が横方向に流れている状況を考えよう。川幅(水路幅)は一定とするので、奥行き方向は考えない。上流からの給水と下流での排水が常に一定で等しい状態、つまり流れが定常状態にあるとする。

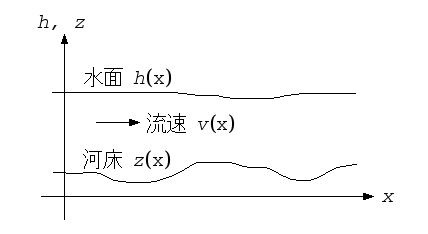
　こういう状況で、任意に河床の形状z(x)が与えられたときに、水面形がどうなるか、計算しよう。

基礎方程式

この問題を扱う出発点として, 以下のような2つの基礎方程式がある:

水面近傍におけるエネルギー保存則(ベルヌーイの定理):

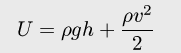.............. (1)

ここで、Uはエネルギー(一定), ρは水の密度、gは重力加速度、hは水面の高さ、vは流速

質量保存則(流量一定):

..................(2)

ここで、qは単位幅流量(一定)、zは河床の高さ

以上の2つの式が、基礎方程式である。

微分方程式

(1)と(2)から、以下の式が導かれる(水面と流速に関する連立微分方程式):

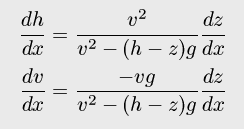......(3)

これが、解くべき微分方程式である。

ちなみに、フルード数Frを導入して(3)を変形すると、

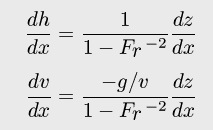............(4)

のようになる。これをみると、フルード数が1に近付くと右辺が発散することがわかる。従って、フルード数が1をまたいで変化するような場合(跳水など)はこの方程式は解けない。

問： (1)(2)より、(3)を導け。 ヒント：　Uやqは、場所xによらない定数なので、xで微分すればゼロになって消える。

問： (3)より、(4)を導け。

数値解析 式(3)は、1階の連立常微分方程式なので、これまで学んだ方法で数値解析できる。

問： 式(3)を、以下の条件で、ルンゲ・クッタ法で解き、結果をグラフにせよ。

h(0)=0.5 [m]
v(0)=1.0 [m/sec]
z(x)=0.1sin(x) [m]
ρ=1000 [kg/m3]
g=9.8 [m/s2]
xは0から10 [m]

ヒント：　河床形状を表現するために、三角関数を使う必要がある。三角関数のような解析関数をC言語で使うには、数学ライブラリを利用する。具体的には、# include <stdio.h>の次の行に、# include <math.h>という行を入れる。コンパイルするときは、gccに-lmというオプションをつけること。

プログラムの例

出力例：

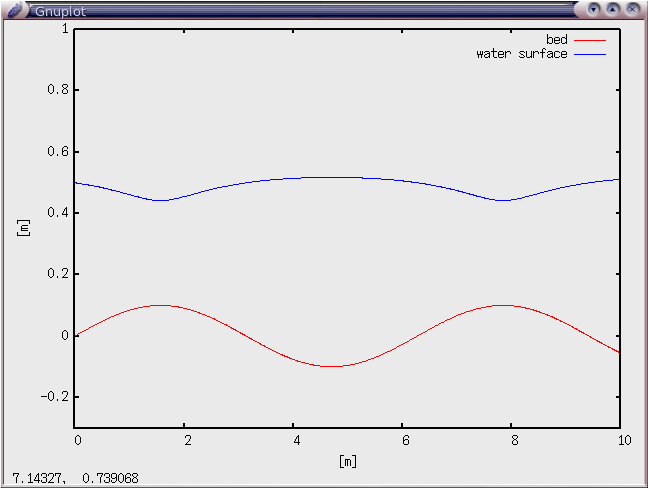
参考： これを描いたGnuplotコマンド

set xlabel [m]
set ylabel [m]
set yrange [-0.3:1]
plot "out" using 1:2 title "bed" w l, \
    "out" using 1:3 title "water surface" w l 3

問： この解のフルード数もプロットしてみよ。

常流と射流

上の条件(常流)と同じエネルギーおよび同じ流量を実現するような、別の解(射流)も存在するはずである。それを見つけてみよう。

問： まず、水深と流速に対してエネルギーを与える式、つまり式(1)を変形して、水深と流量に対してエネルギーを与える式を作れ。ヒント：式(2)を用いて、vをqとhで表す。平均河床を考えて、z=0としてよい。

問： その式を、横軸を水深として縦軸をエネルギーとするグラフにプロットしてみよ。その際、密度ρを入れたままにすると、SI単位系ではエネルギーUが莫大な数字になるので、エネルギーUのかわりに、U/ρを縦軸にとるとよい。

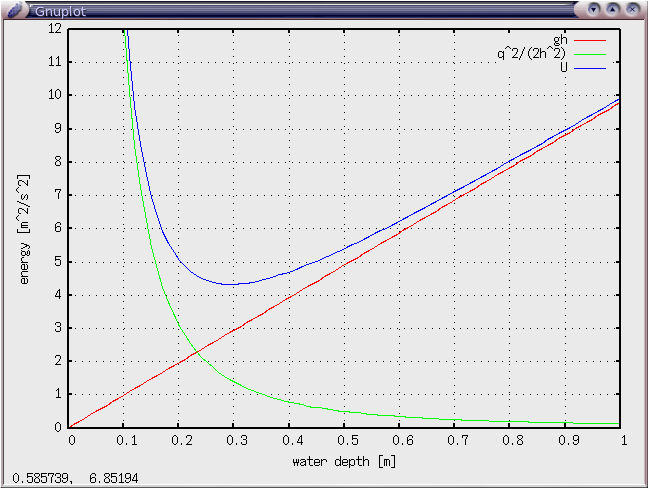
参考： これを描いたgnuplotコマンド

set xrange [0:1.0]
set yrange [0:12]
set xlabel "water depth [m]"
set ylabel "energy [m^2/s^2]"
set xtic 0.1
set ytic 1
plot 9.8*x title "gh", 0.5*0.5/(x*x*2) title "q^2/(2h^2)", 9.8*x+0.5*0.5/(x*x*2) title "U"

　これを見ると、水深0.5 mに対応するエネルギー(縦軸で5.5のあたり)は、水深約0.18 mに対応するエネルギーとおなじくらいであることがわかる。つまり、上の条件で計算したのと同じエネルギーかつ同じ流量を、水深0.18 m程度の流れでも実現できることがわかる。(これが射流)

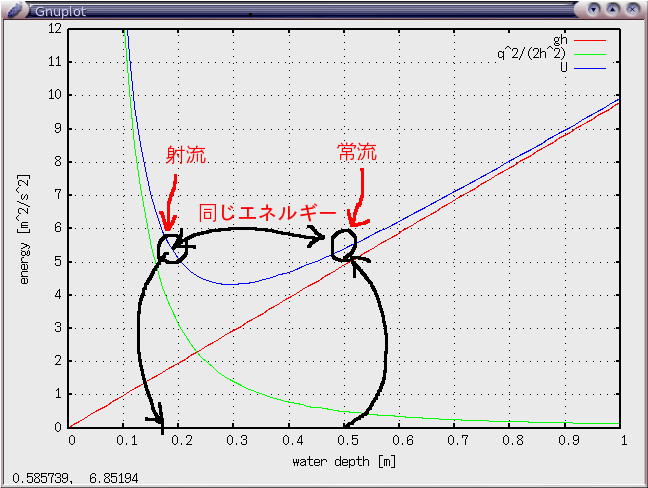
　この射流に対応する(左端での)水深を厳密に求めるには、上で導いたUの式に関する代数方程式を解けば良い。それには、Newton法などを用いる。

問： この射流に対応する(左端での)水深をNewton法で求めよ。

プログラムの例:

/* openchannel.c
 * 2004/01/26 Kenlo Nishida
 * compile: $ gcc openchannel.c -o openchannel -lm
 * usage: Give h and v from stdin.
 */
# include <stdio.h>
# include <stdlib.h>
# include <math.h>
# define NV 2                // number of (dependent) variables for Runge-Kutta solver
# define DX 0.01             // step along x-direction
# define G 9.8               // gravity acceleration
# define rho 1000            // water density [kg/m^3]

double z(double x){          // river bed
   return(0.1*sin(x));}

double dzdx(double x){        // gradient (slope) of the river bed, i.e., dz/dx
   return ( (z(x+DX)-z(x-DX))/(2*DX) );}

void func(double x, double *p, double *dpdx)   // differential equation
 // x: x-coordinate
 // p[0] ... h
 // p[1] ... v
 // dpdx is output
{double h, v;
 h=p[0]; v=p[1];
 dpdx[0] =    dzdx(x)*v*v/(v*v - (h-z(x))*G);     // dh/dx
 dpdx[1] = -1*dzdx(x)*v*G/(v*v - (h-z(x))*G);     // dv/dx
}

void RungeKutta(double x, double dx, double *p){
  double dpdx[NV], dpdx0[NV], dpdx1[NV],dpdx2[NV],dpdx3[NV];
  double                         p1[NV],   p2[NV],   p3[NV];
  int i;
  func(x,      p,  dpdx0); for (i=0; i<NV; i++) p1[i]=p[i]+dpdx0[i]*dx/2;
  func(x+dx/2, p1, dpdx1); for (i=0; i<NV; i++) p2[i]=p[i]+dpdx1[i]*dx/2;
  func(x+dx/2, p2, dpdx2); for (i=0; i<NV; i++) p3[i]=p[i]+dpdx2[i]*dx;
  func(x+dx,   p3, dpdx3);
  for (i=0; i<NV; i++) dpdx[i]=(dpdx0[i] + 2*dpdx1[i] + 2*dpdx2[i] + dpdx3[i])/6;
  for (i=0; i<NV; i++) p[i]=p[i]+dpdx[i]*dx;
}

int main(){ 
double x;
double x0=0, x1=10;      // boundary
double p[NV];
double dx=DX;

// setting initial condition
scanf("%lf", &p[0]);     // h
scanf("%lf", &p[1]);     // v

for (x=x0; x<x1; x=x+dx){
    printf("%lf  %lf  %lf  %lf\n", x, z(x), p[0], p[1]/sqrt(G*(p[0]-z(x))));
    RungeKutta(x, dx, p);
   }
}

その結果、h = 0.187 mが、この射流の条件であることがわかる。

問： この射流(左端での水深は0.187 m)を、上と同様に計算し、プロットしてみよ。

参考になるページ： 開水路 (Wikipedia)