3. スマホを使った統計処理の練習

この実習では緯度経度データを統計処理する。それを屋外でスマホでやる。そのための練習として以下の問題をやろう。スマホのアプリを使ってよい（Androidアプリ「標準偏差計算機」は便利）。答が既に書かれているが, 自分で計算してそうなることを確認すること。

なお, 標準偏差を求めよという問がたくさん出てくるが, ざっくりいえば, それはデータ解析において誤差（不確かさ）を求めることと同義である。標準偏差は誤差（不確かさ）の指標なのだ。

課題3-1（レポートにしなくてよい）: 以下のデータについて,

5, 6, 4, 5, 8, 3, 4

(1) 標本平均を求めよ。 答: 5.0

(2) 標本分散を元に標本標準偏差を求めよ。答: 1.51

(3) 不偏分散を元に標本標準偏差を求めよ。答: 1.63

解説: サンプルサイズをnとすると（この問題では7）, 標本分散は残差平方和をnで割り, 不偏分散は残差平方和をn-1で割る（「大学1年生のための数学入門」参照）。前者より後者のほうが大きい。サンプルサイズが大きい時はこれらの差は気にならないのでどちらを使っても大差はないが, 今回の実習ではサンプルサイズは4~5程度と小さいので, 不偏分散を元にした標本標準偏差を使う。

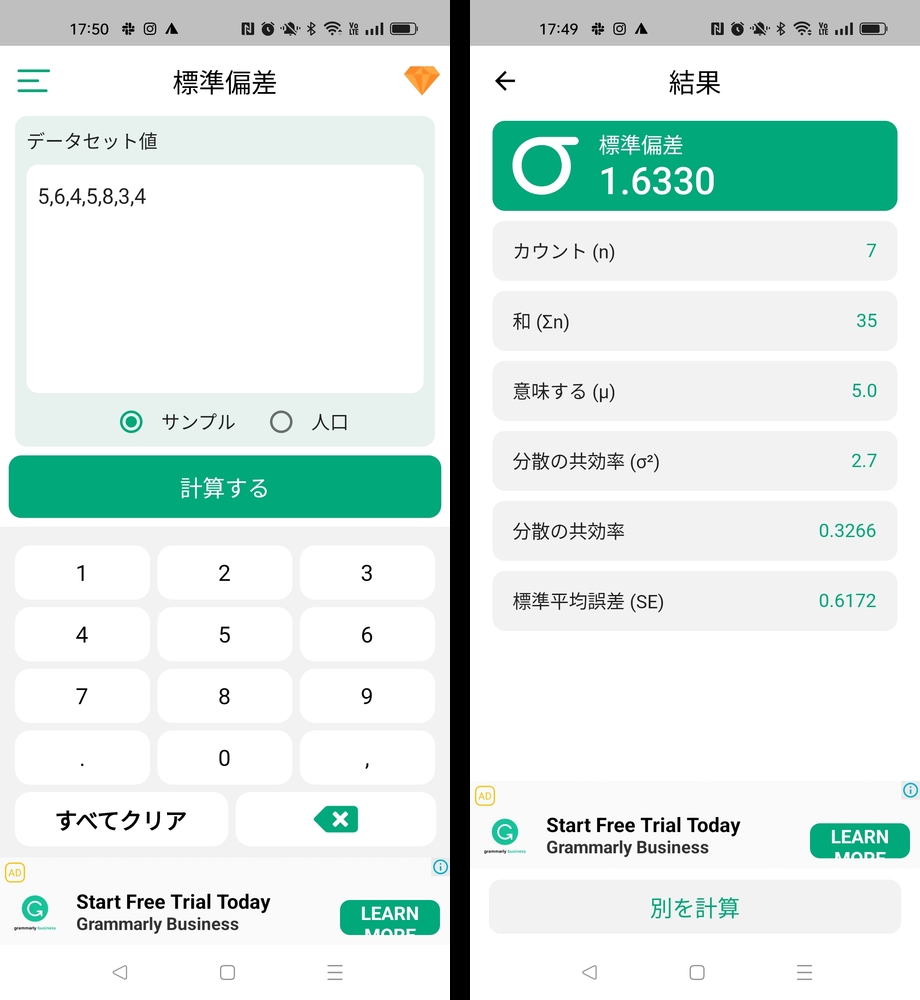
Androidアプリ「標準偏差計算機」でやってみた結果を示す:

↑左の画面の「人口」は"population"の誤訳（正しくは「母集団」）。母集団全体を網羅するデータを扱う場合, という意味であり, すなわち標本分散を用いた標準偏差が出てくる。

↑左の画面の「サンプル」は母集団から抽出した小さな標本（サンプル）を扱う場合, という意味であり, すなわち不偏分散を用いた標準偏差が出てくる。

課題3-2（レポートにしなくてよい）: 以下のデータについて,

4005, 4006, 4004, 4005, 4008, 4003, 4004

(1) 標本平均を求めよ。 答: 4005.0

(2) 標本分散を元に標本標準偏差を求めよ。答: 1.51

(3) 不偏分散を元に標本標準偏差を求めよ。答: 1.63

解説: 問題1と問題2で, (2)以降は同じになった。これは偶然ではない。問題2の各データから4000を引くと問題1のデータになる。そして, 分散や標準偏差は, このようにデータから一律に値を引いても変わらないのだ（理由は分散や標準偏差の定義に戻って考えればわかる）。このことはこの後の問題でも利用できる。

問題3-3（レポートにしなくてよい）: 以下の緯度・経度を, 度の小数だけで表わせ:

N 36 deg 5 min 1.72 sec, E 140 deg 7 min 0.51 sec

答: N 36.083811 deg, E 140.116808 deg

解説: 秒から計算すると楽。まず1.72を60で割って, 5を足して, 60で割って, 36を足す。

問題3-4（レポートにしなくてよい）: 以下の緯度・経度を, 度分秒で表わせ:

N 36.12215 deg, E 140.31245 deg

答: N 36 deg 7 min 19.74 sec, E 140 deg 18 min 44.82 sec

解説: まず度の整数部分はそのまま。1未満の小数を計算機に入れ60をかける。その整数部が分。その整数を引いて（1未満の小数になる）60をかけると秒が出る。

問題3-5（レポートにしなくてよい）: 以下の地点について,

N 36 deg 5 min 1.72 sec, E 140 deg 7 min 0.51 sec

N 36 deg 5 min 1.93 sec, E 140 deg 7 min 0.23 sec

N 36 deg 5 min 1.54 sec, E 140 deg 6 min 59.87 sec

N 36 deg 5 min 1.36 sec, E 140 deg 6 min 59.28 sec

N 36 deg 5 min 1.66 sec, E 140 deg 7 min 0.04 sec

(1) 緯度の標本平均を求めよ。答: N 36 deg 5 min 1.64 sec

解説: N 36 deg 5 minまでは同じなので, secの数値だけを平均すればよい。なぜ? 同じ値をn個足してnで割っても同じ値が出てくるだけだから!

(2) 経度の標本平均を求めよ。答: E 140 deg 6 min 59.99 sec

解説: minの値が6と7にわかれるが, たとえば6 min 59.87 secは7 min -0.13 secとみなせばよい。

(3) 緯度の標本標準偏差を求めよ。(不偏分散を元に)　答: 0.212 sec

解説: (1)と同様に, secの値だけで計算すればよい。その理由は上の問題2。

(4) 経度の標本標準偏差を求めよ。(不偏分散を元に) 答: 0.461 sec

問題3-6（レポートにしなくてよい）: 位置の有効数字について考えよう。なお, 赤道で地球1周はほぼ4万 kmである。

(1) 緯度の差0.1秒は何mに相当するか? 答: 3.1 m

(2) 経度の差0.1秒は何mに相当するか? 答: 緯度による。北緯35度なら2.5 m。

(3) 緯度の誤差が約3 cmの場合, それは約何秒に相当するか? 答: (1)において, 3.1 mの1/100が約3 cmだから, 0.1秒の1/100, すなわち0.001秒。

解説: まず赤道で緯度360度が4万 kmに相当するので, 緯度1度に相当するのは4万 km/360=111.1 km。1度は3600秒なので, 1秒に相当するのは111.1 km/3600=0.0309 km = 30.9 m。従って0.1秒は3.09 m ≒ 3.1 m。ところが経線の間隔は地軸からの距離に比例するので高緯度ほど狭い。地軸からの距離は緯度のコサインに比例する。従って北緯35度なら, 経度0.1秒に相当するのは3.09 m x cos(35度) = 3.09 m x 0.819 = 2.5 m。

解説: GNSS-RTKは位置の測定誤差が数cm程度, すなわち(3)で見た0.001秒のオーダーである。ということは, GNSS-RTKで得たデータは, 0.001秒の桁（あるいは余裕をもってもうひと桁）まで記録する必要がある。

同じ場所で何回か位置を計測した際, その標本標準偏差が計測の誤差（不確かさ）のひとつの目安になるのだ。

戻る