6. GNSS単独測位

　ではGNSSで実際に位置計測をしてみよう。スマホでできるのは「単独測位」という方法である。ちなみに先述したようにGNSSは衛星からの電波が届かない場所では役立たない。特に鉄筋コンクリートの建物の奥深くや地下などは厳しい。屋外であっても建物や樹木のそばだと, そっち方向にいる衛星からの電波が来ない。一方, 屋内でも電波がスカスカに届く建物なら大丈夫だ。ビニールハウスやテントの中は問題ない。鉄筋コンクリートの建物でも窓際に行けば, そこそこいける。諸君にはGNSSがイケる場所とイケない場所がどういう場所かを実体験で掴んで欲しい。

課題6-1: GNSS単独測位を行うアプリを各自のスマホに入れよ。以下をお勧めする。各メンバーが何を入れたかレポートで述べよ。
課題6-2（レポートにする必要はない）: 入れたアプリで, 以下のことを表示・操作してみよ。班の中で助け合い, 全員が表示できるようにせよ。

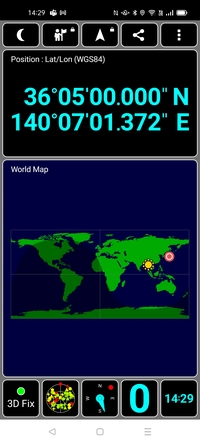
(1) 緯度と経度

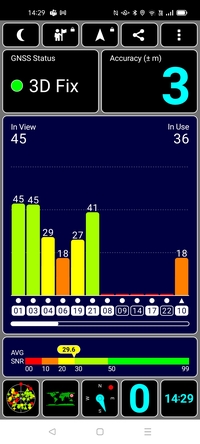
(2) 補足した衛星の数（20個〜40個くらいあるはず）

(3) 補足した衛星の空中での位置（星座早見表みたいな図）

(4) 位置精度（メートル単位で出てくるはず）

(5) 時刻（GNSS衛星の電波には時刻情報が入っている。それは極めて高精度であり標準時計のかわりにできる）

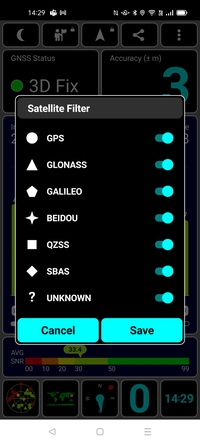
(6) 補足する衛星の種類を変えたり絞ったり（GPSだけにしたり, QZSSだけにしたり）。

課題6-3: 補足する衛星の数や位置精度は, 電波の受信状況によって変わる。建物の中や木の幹の側, 人の体で覆いかぶさったり, いろいろ工夫して補足衛星数を減らしてみよ。それに伴って位置精度はどう変化するか?

課題6-4: 受信状況の良い場所を選んで, 緯度経度情報の数値の変化を観察せよ。秒の小数点以下が時々刻々と変わっていくだろう。1分間くらい観察し, その変動幅はざっくりどのくらいか秒単位で答えよ。それを仲間の結果（計測場所は互いに数mくらい離れていてもよい）と比べよ。異様に小さい人や異様に大きい人はいるか? いたらその理由を考えてみよ。

課題6-5: 地図上で再現可能な場所（何かの真ん前とか道の曲がり角とか）を選んで, そこで全員が（交代しながら同じ場所で）緯度・経度を計測し, 共有・記録せよ。

課題6-6: メンバー全員のデータから, 緯度と経度の標本平均を求めよ。

課題6-7: メンバー全員のデータから, 緯度と経度の標本標準偏差を求めよ。不偏分散から求めよ。

課題6-8: その標本標準偏差は, 距離にすると何メートルか? ヒント: 問題3-6

課題6-9: その標本標準偏差をアプリが表示する位置精度と比較せよ。どちらがどのくらい大きいか?

課題6-10: その場所を国土地理院のウェブマップサービスうぉっちずで表示し, うぉっちず上での緯度経度を調べよ。

↑「うぉっちず」でキャンパス内の橋の緯度経度を表示したところ。

課題6-11: 課題6-6と課題6-10の結果を比較せよ。誤差は距離にするとどのくらいか? それを課題6-8で得た標本標準偏差や, 課題6-9で得た位置精度と比較し検討せよ。

課題6-12（オプション）: メンバー全員の緯度経度計測値（確率変数とみなす）は互いに独立と言えるだろうか? 独立性を妨げる要因があるとしたら何か? 話し合え。

課題6-13（オプション）: メンバー全員の緯度経度計測値は互いに独立と仮定して（たとえ無理があっても目をつぶって）, 緯度・経度の標準誤差を求めよ。標準偏差は標本標準偏差を使えばよい。標準誤差を1 m未満にするには, 計測の反復回数を何回くらいにすべきか?（大数の法則）

ここで君は大きな教訓を得たはずだ。統計学は野外計測の精度評価において有用であり必須なのだ。特に, 標準偏差によって誤差の大きさを評価したり, 反復によって誤差を小さくするには大数の法則など, 「統計学入門」や「実用解析I」で学んだことが役立つのだ。

戻る