7. GNSS単独測位(標高)
GNSSは標高も計測できる。ただし, GNSSが計測するのは標高ではなく「楕円体高」というものである。これは地球を回転楕円体と近似し, そこからの距離である。それに対して, 標高は「ジオイド」(地球の重力の等ポテンシャルエネルギー面のひとつであり, 平均海水面に近いもの)からの距離である(1年次「物理学」でやった!)。ジオイドは回転楕円体よりも上にあることも下にあることもある。回転楕円体から見たジオイドの高さを「ジオイド高」という。つまり, 「楕円体高 = ジオイド高 + 標高」である。ということは,
「標高 = 楕円体高 - ジオイド高」

だから, その場のジオイド高がわかればGNSS計測された楕円体高から標高がわかる!!
注: 「ジオイド高」は「ジオイドからの高さ」ではなく, 「楕円体からジオイドまでの距離」つまり「ジオイドの楕円体高」である。まぎらわしいが注意しよう。
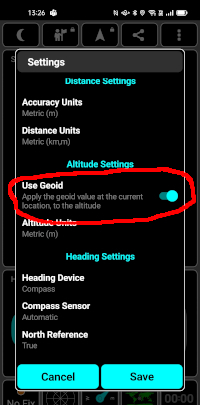
地球全体でジオイド高はどこがどのへんかは概ねわかっている(測地学者ありがとう!)。そのデータは君のスマホのそのアプリにも入っているはずだ。だから, アプリで「標高」と「楕円体高」を切り替えて表示できるだろう。GPSTestでは, ↓この"Use Geoid"を有効にするとジオイドからの高さ, つまり標高になる。
課題7-1: 君のアプリを使って, 現在地の標高を求めよ。(筑波大学キャンパスでは約25 mのはず)
課題7-2: 君のアプリを使って, 現在地の楕円体高を求めよ。(課題7-1よりだいぶ大きい値のはず)
課題7-3: ジオイド高を筑波大学キャンパス周辺では約40mとし, 「標高 = 楕円体高 - ジオイド高」の式が成り立っているか確認せよ。なお, パソコンがあればこのサイトでジオイド高を調べることができる。
ここで君は大きな教訓を得たはずだ。スマホで「標高」を計測したとき, それがほんとに「標高」なのか, それとも「楕円体高」なのか, そこを誤解すると, 大きな間違いをしてしまう(40mもずれる!!)ということだ。こういうことをちゃんとわかって対処できるかどうかが「しっかりした人」のひとつのポイントである。1年次の「物理学」でポテンシャルエネルギーを学んだのはこの伏線だったのである。
課題7-4(オプション): 仲間の標高計測値を集めて, 標本平均・標本標準偏差・標準誤差を求めよ。
課題7-5(オプション): そのアプリで歩道橋の高さを計測してみよう。歩道橋のたもとと歩道橋の上でそれぞれ標高を測り, その差で歩道橋の高さを求めよ。班員全員がそれぞれ行って, 標本平均・標本標準偏差・標準誤差を求めよ。
課題7-6(オプション): 課題7-4の標準誤差と課題7-5の標準誤差を比べてみよう。課題7-5は2つの標高の差を測っているので, 誤差伝播の法則(V[X-Y]=V[X+(-Y)]=V[X]+V[-Y]=V[X]+V[Y])から, それぞれの標高(橋のたもとと上)の誤差の2乗どうしの和の平方根となる。ここでは誤差として標準誤差を用いると, たもとも頂上もほぼ同様に課題7-4の標準誤差を仮定すれば, 課題7-4の標準誤差の√2倍が課題7-5の標準誤差になるはずだ(ただし誤差同士が独立ならば!!)。実際そうなっているかどうか調べよ。
戻る


