C言語による微分方程式の解析 (Runge-Kutta法)

筑波大学農林工学系　奈佐原顕郎

　オイラー法は精度がよくない。刻み幅dtを小さくすれば精度は上がるが, そのぶん, 計算時間がかかる。精度が悪いのは, ひとつのステップを進むときにdx/dtをステップの最初のときの状態から計算しているので, 途中の尻上がり的な(または尻下がり的な)変化にうまく対応できず, 誤差がどんどん蓄積するためである。

　そこで, dx/dtの推定を, もう少し念入りにやってやれば, 精度はよくなると思われる。そこを改良したのが, Runge-Kutta (ルンゲ・クッタ)法である。この方法のコンセプトは, dx/dtをいっぱつで求めるのではなく, 以下のようにする:

1. まずとりあえずのdx/dtを現在値から計算 (それをk0とおく)。
2. その推定値k0を使って, tから半ステップだけ(dt/2), xをとりあえず進める (それをx1とおく)。
3. そのx1を使って, t+dt/2におけるdx/dtを計算 (それをk1とおく)。k1はk0よりもましなdx/dtの推定値である可能性が高い。
4. そのk1を使って, tから半ステップ(dt/2)だけ進んだxをもういちど求める (それをx2とおく)。
5. そのx2を使って, もういちどt+dt/2におけるdx/dtを計算 (それをk2とおく)。
6. そのk2を使って, こんどはtからいちステップ(dt)だけ進んだxを求める (それをx3とおく)。
7. そのx3を使って, t+dtにおけるdx/dtの推定値 (それをk3とおく)を計算する。
8. 以上で, dx/dtの推定値として, k0, k1, k2, k3という4つの値が求まる。それを以下のように加重平均したものを, 正式な, dx/dtの推定値 (それをkとおく)とする：

   k=(k0 + 2*k1 + 2*k2 + k3)/6

そのkを使って, t+dtにおけるxを最終決定する。

　要するに, まず傾きを求め, 半歩進んで傾きを求めて半歩戻り, また半歩進んで傾きを求めて半歩戻り, 1歩進んで傾きを求めて1歩戻り, それぞれの傾きを1,2,2,1の重みで平均し, それを最も正確な傾きと仮定して, 1歩進む。それがRunge-Kutta法である。

　ややこしいように見えるかも知れないが(私も最初はややこしいと思った!), よく考えるうちに慣れるものである。

　さてこの方法で, 前回のeuler1.cと同じ解析(dx/dt = 2x; t=0のときx=1)をやってみよう:

/* RK1.c */
/* Runge-Kutta */
/* 2004/2/15 K. Nishida */
# include <stdio.h>
main()
{
double t=0;
double dt=0.1;
double x=1;
double x1, x2, x3;
double k0, k1, k2, k3;
double dx;
printf("%lf %lf\n", t, x);
for (t=dt; t<=1; t=t+dt)
{k0=2*x;
x1=x+k0*dt/2;
k1=2*x1;
x2=x+k1*dt/2;
k2=2*x2;
x3=x+k2*dt;
k3=2*x3;
dx = dt*(k0 + 2*k1 + 2*k2 + k3)/6;
x=x+dx;
printf("%lf %lf\n", t, x);
}
}

注意: 左端の数字（6.など）は打ち込まないで良い。

　では, 同じdtの刻みで結果がどう違うか, 見てみよう：

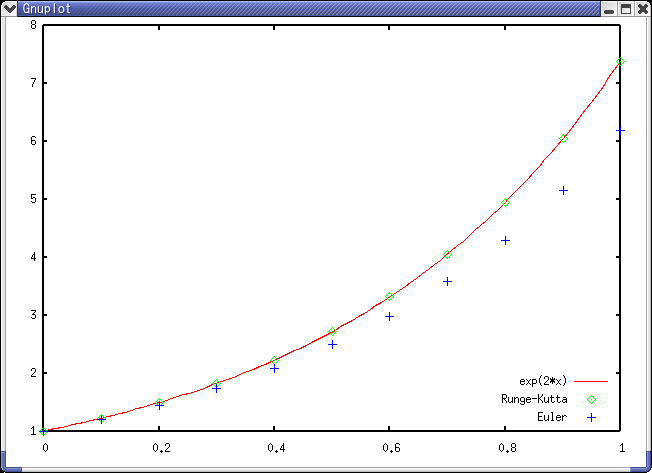
↑ dt=0.1のとき(赤線が理論解)

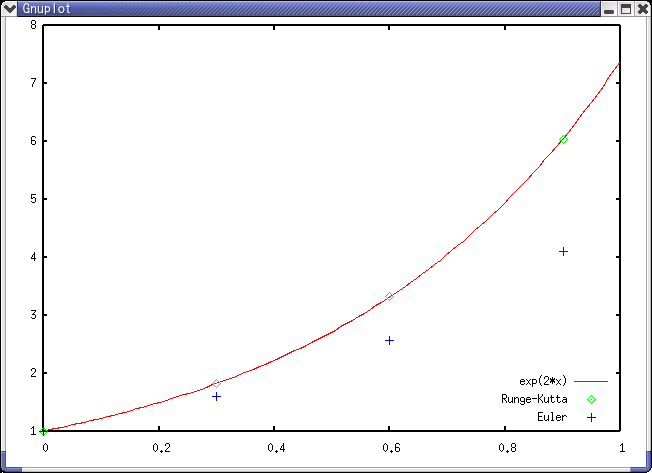
↑ dt=0.3のとき(赤線が理論解)

　上のグラフを見ればわかるように, Euler法は刻み幅(dt)を荒くするとどんどん精度が落ちるが, Runge-Kutta法は, ほとんど理論解から離れず, 驚異的な精度を保っていることがわかる。

課題14-1： Logistic方程式の解析プログラム(課題13-1)をRunge-Kutta法に改造してみよ。

課題14-2： バネの振動運動の解析プログラム(前回のeuler2.c)をRunge-Kutta法に改造してみよ。

（ブラウザの「戻る」ボタンで戻ってください。）