Newton法で代数方程式を解こう

筑波大学農林工学系　西田顕郎

　Newton法とは、代数方程式f(x)=0を数値的に解く方法のひとつである。

　関数y=f(x)のグラフを考えよう。

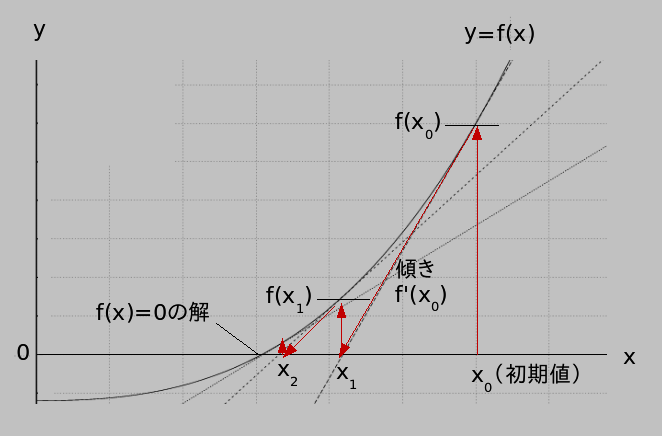
　まず、初期値、つまりy=f(x)=0の解の候補として、適当な数をx₀として与える。このときf(x₀)は、もちろん、ゼロとは限らない。

　そこで、点(x₀,f(x₀))を考え、その点における、y=f(x)の接線を求めると、次式のようになる：

y=f'(x₀)(x-x₀)+f(x₀)

　この接線（つまり直線）がx軸と交わる場所をx=x1として求めると、次式のようになる：

x₁=x₀-f(x₀)/f'(x₀)

　上の図を見たらわかるように、x₁は、x₀よりも、解に近付いている。この操作を何回か繰り返せば、解にたどりつくことができるだろう。それがNewton法である。

例題: x³+4x²-6=0をニュートン法で解け。

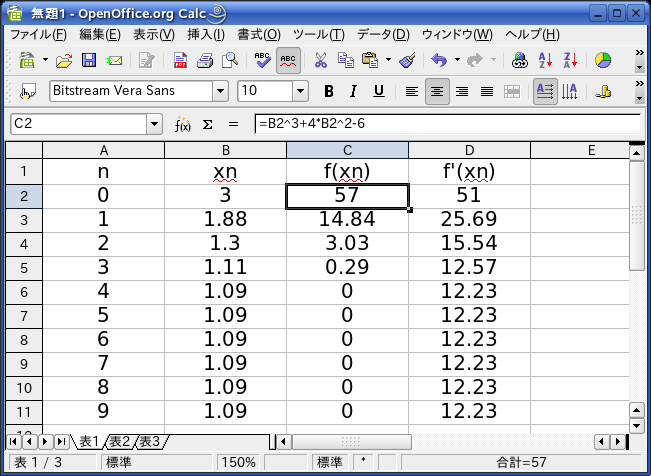
　ここで、左端のA列は、x_nのnを表すが、計算には関与しない（単なるラベルである）。

　セルB2に、初期値を入れる。この初期値は、人間が適当に決めるのである。この「適当」というのは、ほんとに「適当」としか言いようがない。「だいたいこんなもんでいいだろう」という値を、人間の頭で判断して放りこむのである。

　セルC2には、セルB2をxとするようなf(x)の計算式を入れる。ここでは、"=B2^3+4*B2^2-6"とすればよい。

　セルD2には、セルB2をxとするようなf'(x)の計算式を入れる。ここでは、"=3*B2^2+8*B2"とすればよい。

　セルB3には、x₁を与える計算式、つまり、"=B2-C2/D2"を入れる。

　あとは、セルB3をB列の下の方までコピーペースト、セルC2をC列の下の方までコピーペースト、セルD2をD列の下の方までコピーペーストすればよい。

　そうすると、n=3かn=4くらいで、十分な精度でf(x)=0の解がB列に表示される。

　このように、Newton法は、適当な初期値から出発して、y=f(x)の接線とx軸の交点を逐次、求めることで、解に迫っていく。その迫りぐあいは、かなり早い。10回も繰り返せば、たいていの場合は、十分な精度で解に収束する。

　ところが、Newton法の弱点として、複数の解を持つような代数方程式に対して、どの解を求めるかによって初期値を人間が適切に判断しなければならない、ということがある。

課題4-1. 上の方程式の解を、初期値x=-1でやりなおしてみよ。どのような解が得られるか？その理由を考察せよ。上の方程式の全ての解（3つある）を求めるには、どうすればよいだろうか?

　Newton法のもうひとつの弱点は、導関数（つまり微分）が、あらかじめ解析的に得られるような関数しか相手にできないということである。従って、微分不可能な点、特に不連続点を含むような関数の根を求めるには、なんらかの工夫（解析範囲を絞るとか、初期値をうまく与えるとか）が必要だったりする。

課題4-2. Newton法で、2の平方根、つまりx²-2=0の解を数値的に求めよ(1.4142...になることを確かめよ)。